入試で差がつく! 数式問題で発想力を鍛える理由
中学数学「数式」分野で得点を伸ばすためには、単なる計算力よりも 式の構造を見抜く力 が重要です。
式の中にはいつも“隠れた形”があります。
因数分解や式の変形がうまくいかないのは、計算が苦手だからではなく、
共通の形・対称性・つながりを見抜けていないだけなのです。
「式の構造」を観察する力こそ得点のカギ
数式問題を解くときは、まず手を動かす前に次のようなポイントを意識してみましょう:
- 共通のかたまりはないか
- 二乗や差の形にできないか
- 文字の並びに規則はないか
このように 式を“読む”力 をつけることが、因数分解や式の整理の第一歩です。
実際の問題で考え方を体感しよう
まずは用意したチャレンジ問題に取り組んでみましょう。
式を見てすぐに手を動かすのではなく、まず構造を観察してみましょう。
・共通のかたまりがないか
・二乗や差の形にできないか
・文字の並びに規則はないか
式を“読む”力こそ、因数分解の第一歩です。
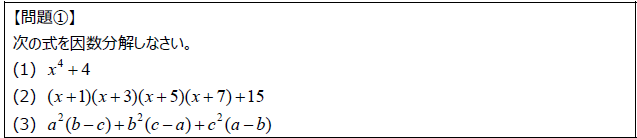
詳しい解説と解答は、こちらからダウンロードしてください。
因数分解は、暗記や計算ではなく発見の練習です。
・A²−B²の形を作る
・かたまりでくくる
・パターンを見つけて再配置する
――こうした小さな発想の積み重ねが、「見抜く力」を育てます。
更に力を伸ばしたい人へ:ドリルのご案内
もっと数式分野の得点力を上げたい人のために、
noteに数式問題編のドリル(有料)を用意しています。
因数分解・方程式・整数条件・文章題など、入試本番でも差がつく問題を厳選。
「どこを見て、どう整理すればよいか」を丁寧に解説しています。
読むだけでも式の“構造を読む力”が鍛えられます!
noteでは「数式」「関数」「平面図形」「空間図形」「場合の数・確率」の各分野でドリルを公開中。
苦手分野を集中して克服したい人も、体系的に学び直したい人も、
解き方が見つかる!中学数学「目のつけどころ」ドリル集をぜひチェックしてみてください。