すうがくパパ
こんにちは、すうがくパパです。
学校で「素因数分解」を習ったとき、「いくつか数字を分解して終わり。これって何に使うの?」と思ったことはありませんか?
でも実はとっても役立つんです!
Contents
最大公約数と最小公倍数を素因数分解で求める方法
最大公約数や最小公倍数の問題を考えるとき、素因数分解は大変便利です。
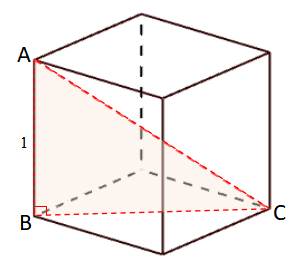
例えば「60と96の最大公約数」を求めたいとき。
それぞれ素因数分解すると、
\(60=2^2\times3\times5\)
\(96=2^5\times3\)
となります。
このとき「両方に共通する因数」をできるだけたくさん集めたものが、最大公約数になります。
つまり、 \( 2^2\times3=12\) が答え!
逆に、最小公倍数を求めるときは、「どちらかに出てくる素因数のうち、指数が大きい方」を全部集めて、
\(2^5\times3\times5=480\)と求められます。素因数分解を使うと、こうした計算があっという間にできちゃいます!
約数の個数を数えるときも素因数分解が活躍!
次に、「60の約数は何個ある?」という問題を考えてみましょう。
まずは素因数分解
なので、60の約数は、2, 3, 5をいくつ含むかに応じて、必ず以下の式で表すことができます。(ここで、含まない場合を「ゼロ乗(=1)」として扱うのがミソです。)
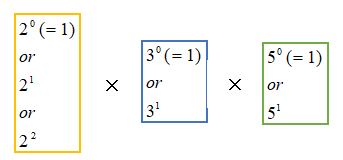
ここで、2の「含み方」は3通り、3の「含み方」は2通り、5の「含み方」は2通りありますので、約数の数は、これらの組み合わせの数となり、3×2×2=12通りとなるのです。
小さい数なら数えてもいいけれど、大きな数になると素因数分解がないととても大変。
ぜひこのやり方をマスターしておきましょう!
公式ではなく“構造”で考える力をつけよう
素因数分解は、ただの計算じゃありません。
数の中にある「しくみ」を見つける道具なんです。
たとえば、60を分けると2や3や5が出てくる。
どんな数も、こうした小さな部品の組み合わせでできているとわかります。
こうして数のしくみを整理して考える力がつくと、
新しい問題に出会っても、自分で道を見つけられるようになります。
「どうしてこうなるんだろう?」――その気持ちを大事にしましょう。
次のステップへ!応用問題で発想をレベルアップ!
ここまで読んだあなたは、
もう「数のしくみを見抜く力」を手に入れています!
次のステップ入試レベルの数式問題にチャレンジ!では、
その力を使って応用問題にチャレンジ!
ただ解くだけでなく、どう考えればスッキリ整理できるかを学べます。
発想を一段レベルアップさせて、自分の考え方を磨いていきましょう。
各分野で入試レベルの問題を厳選!
また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる!中学数学「目のつけどころ」ドリル集
を公開しています(有料)。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます!
ぜひ見に来てください!