
すうがくパパ
こんにちは、すうがくパパです。
中学数学の中でも、空間図形は苦手に感じる人が多い単元です。
「立体が頭に浮かばない」「どこで三平方の定理を使えばいいかわからない」——そんな悩みを解消するには、“平面を切り出して考える発想”が欠かせません。
この記事では、空間図形を得意にするための考え方を、立方体を例にわかりやすく解説します。
Contents
立方体の対角線の長さを解いてみよう:まずは底面で考える
ここでは、立方体の対角線の長さを解く問題を考えてみましょう。
一辺の長さを1とします。この図で対角線は、ACの長さを考えることになります。
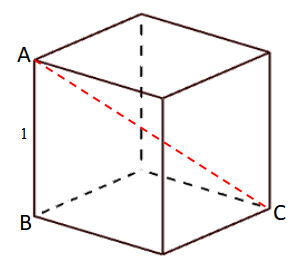
ここで重要なのは、空間をながめるだけでは分からないので、平面を切り出して考えてみることです。
今回は直角三角形ABC(を含む平面)を切り出して考えることで、
直角三角形の辺の長さとしてACを求めればよいと分かります。
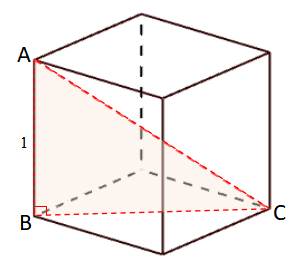
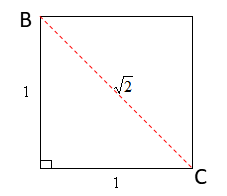
ここで辺BCの長さが問題になりますが、今度は立方体の底面を切り出すと、
底面が正方形になっているので、三平方の定理から
\(BC=\displaystyle\sqrt{1^2+1^2} =\sqrt2 \)
と分かります。
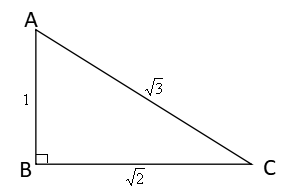
次に高さを組み合わせる
すると、\(AB=1\)、\(BC=\sqrt2\)から、三平方の定理より
\(AC^2=AB^2+BC^2\)なので
\(AC=\sqrt3\)と分かります。
立体を“平面に分けて考える”発想を身につけよう
このように空間図形では、平面図形を切り出して三平方の定理を何回か使うことがコツになります。
マスターすると、こんな問題も簡単に解けますよ!
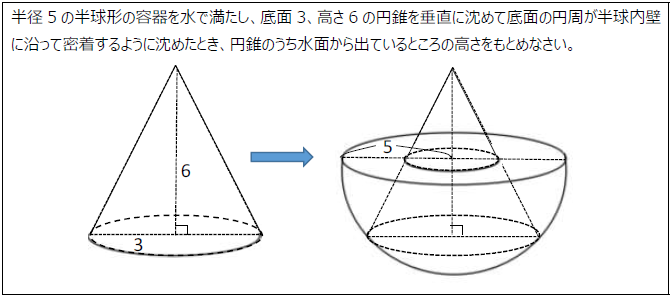
このケースでは、半球の中心をOとして、
Oと円錐の頂点を通り、円錐を垂直に切った断面(平面)を考えるとよいです。
この断面は以下のように二等辺三角形ができます。
ここで重要なのは、円錐の底面が半球の内壁に密着しているので、
半球の中心Oと円錐の底面の円周との距離が半球の半径(=5)になる点です。
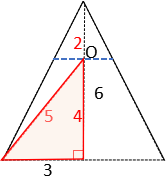
気づくのがポイント!
そこで、赤い直角三角形に注目すると、
底辺が3(円錐の半径)、斜辺が5(半球の半径)なので、
三平方の定理より三角すいのうち水面より下の部分は4となり、
水面から出ている部分は6-4=2と解けます。
次のステップへ!応用問題で発想をレベルアップ!
立体の中で“見えない線”を見つけられるようになると、
空間図形の問題がぐっと解きやすくなります。
三平方の定理の使い方を覚えたら、
次はその発想を使って、もう一歩難しい応用問題に挑戦!
空間の中の点と点の距離を考える問題を通して、
「どこから考えるか」を自分で見つける練習ができます。
入試レベルの問題にもチャレンジ!
また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる!中学数学「目のつけどころ」ドリル集
を公開しています(有料)。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます!
ぜひ見に来てください!


