
すうがくパパ
こんにちは、すうがくパパです。
みなさんは、三角形の「重心」って知っていますか?
図形の問題を解くための着想力アップに、ぜひ「重心」の特徴をおさえておきましょう!
重心がつくる2:1の関係を確認しよう
三角形の各頂点から、反対側の辺の まん中(中点) に線を引きます。
この線を 中線 といいます。
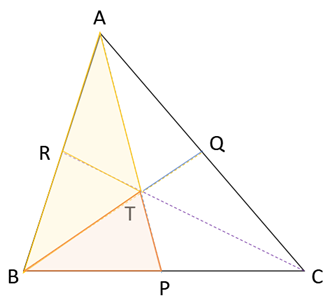
3 本の中線がちょうど交わるところが 重心 。この図ではTが重心です。
ここで重要な数字が 2:1!
頂点Aから重心Tまでの長さ:重心Tから中点Pまでの長さが2:1、つまりAT:TP=2:1になります。
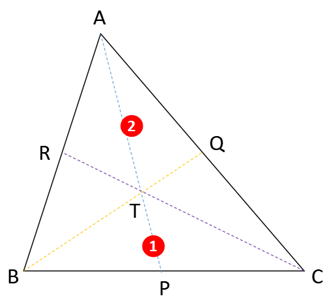
他の頂点でも同じで BT:TQ=2:1, CT:TR=2:1になります。
でも、なぜ2:1になるんでしょうか?
いっしょに考えてみましょう!
相似を使って2:1を説明する方法
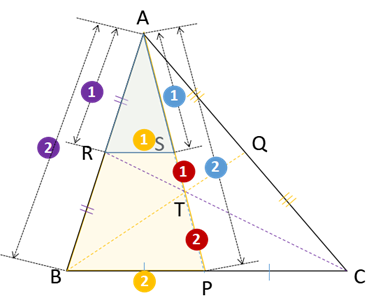
この図で重要な特徴は、P、Q、Rとも各辺の中点だということ。
ということは、AR:AB=AQ:AC=1:2が成り立ち、△ARQと△ABCは相似になりますね。
だからRQ//BCも成り立ち、RQ:BCも1:2になります。
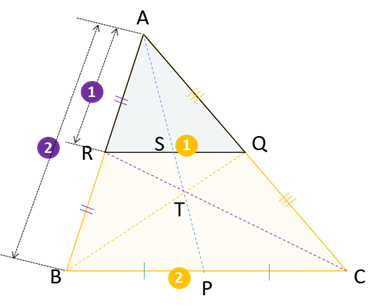
ということは、ここでAPとRQの交点をSとすると、
△ARSと△ABPも相似になって、AS:AP=RS:BP=1:2が成り立ちます。・・・①
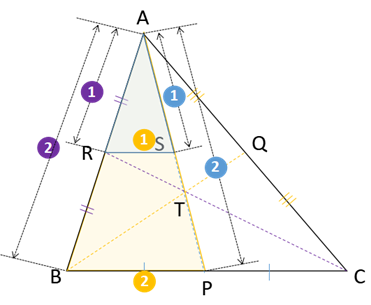
さらに、BP=PCで、RS(1/2BP) =SQ(1/2PC)なので、
△STQと△TBPは相似になり、ST:TP=SQ:BP =1:2になります。・・・②
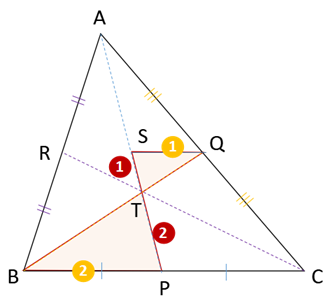
以上を整理すると、
①よりAS:AP=1:2 (AS:SP=1:1になります)
②よりST:TP=1:2
になるので、AS:ST:TP=3:1:2と整理できます。
したがって、
AT:TP=4:2=2:1になります。
このように、図形の相似に目をつけることで「2:1」を説明できましたね!
面積を使って2:1を証明してみよう
相似ではなく、図形(三角形)の面積に目をつける方法もあります。
まず、△ABCを中線で二つの三角形に分けてみます。
すると、BP=PCなので、△ABPと△APCの面積は等しいですね。
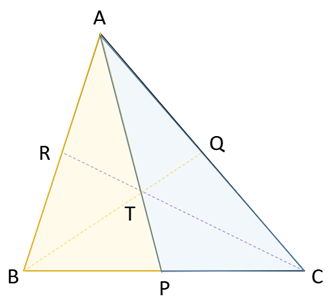
しかも、BP=PCということは、△TBPと△TPCの面積も等しくなります。
したがって、
△ABT(△ABP-△TBP)と△ATC(△APC-△TPC)の面積も等しいです。
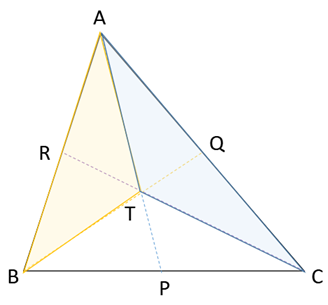
等しいことも分かります
さて、今度は辺ABを底辺とみなして同じように考えると、△ATCと△TBCの面積が等しいということになります。
つまり、重心から各頂点に引いた線で分けられた三つの三角形
△ABT・△TBC・△ATCは面積が等しいのです。
さらに、それぞれの三角形は、重心と中点を結ぶ線で面積が二分されているので、
結局、△ABCを3本の中線で分けた6つの三角形はすべて面積が等しくなります。
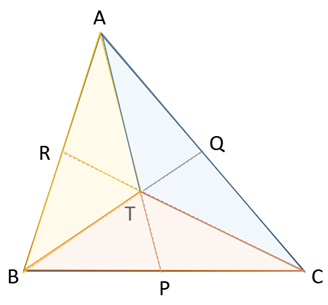
そこで、△ABCの左半分となる△ABPに注目します。
△ART、△RBT、△TBPに分けられていますが、三つとも面積は等しいです。
ということは、
△ABPの面積は△TBPの3倍ですね!
ここで、△ABPと△TBPは底辺BPが共通するので、高さは3:1になります。
つまりAP:TP=3:1であり、AT:TP=2:1になります。
次のステップへ!応用問題で発想をレベルアップ!
重心の2:1を理解できたあなたは、
もう図形の中にある“比”を見抜く力を持っています!
次は、少しレベルアップした問題に挑戦!
平行や相似を使って、台形や三角形の面積比を考える応用問題に取り組めます。
「どこから考えればいいの?」という迷いが、
“発想のヒント”に変わる感覚を体験してみてください。
入試レベルの問題にチャレンジ!
また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる!中学数学「目のつけどころ」ドリル集
を公開しています(有料)。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます!
ぜひ見に来てください!

