空間図形の問題が難しく感じる理由は、
公式や計算が分からないからではありません。
多くの場合、
- どこに注目すればよいのか
- 何から考え始めればよいのか
という「考え始めの一手」で止まっています。
立体はそのまま見続けない
空間図形では、立体を立体のまま考え続けるとうまくいきません。
- 上から・横から見た図を描く
- ある平面で切って断面を考える
といったように、視点を変える・切り出すことが最初の一歩です。
量を直接求めにいかない
長さ・面積・体積を、いきなり求めようとしないことも重要です。
- その量は、何が分かれば計算できるのか
- どの図形に注目すればよいのか
を先に考えます。
高さが分からなければ垂線を下ろし、
体積が出せなければ立体を分けて考える――
空間図形では、遠回りに見える操作が近道になります。
実践問題にチャレンジ!
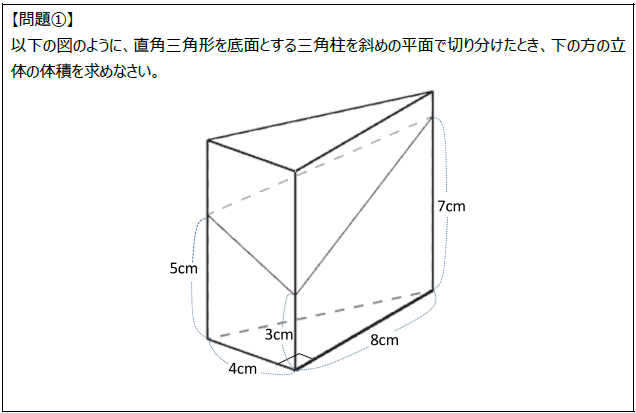
例えば、こちらの問題で「目のつけどころ」を考えてみましょう。
どのように解きますか?
詳しい解説と解答は、こちらからダウンロードしてください。
空間図形は、数をこなすよりも
見方を知ることで一気に解けるようになる分野です。
「公式は分かるのに解けない」と感じている人ほど、
ぜひ一度、見方そのものを確認してみてください。
ドリルで「目のつけどころ」を鍛えよう!
さらに、「空間図形」で本格的に得点力を伸ばしたい人のために、
noteでは空間図形編のドリル(有料)を用意しています。
入試本番で頻出の立体問題を厳選し、
「どの平面に注目すればよいか」「どんな補助線を引くべきか」を丁寧に解説。
読むだけでも空間認識力が鍛えられます!
また、noteでは「数式」「関数」「平面図形」「空間図形」「場合の数・確率」の
各分野のドリルも公開中です。
苦手分野を集中的に鍛えたい人も、体系的に学び直したい人も――
解き方が見つかる!中学数学「目のつけどころ」ドリル集をぜひチェックしてみてください。

