数学の問題を解くときの「目のつけどころ」って何？（その2）

前回（その1）では、数学の問題を解くときの「目のつけどころ」とは、
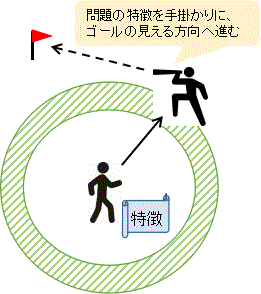
問題に書かれている「特徴」を手がかりに、「さらに分かることがないか」と考えを進めていくこと
だとお話しました。

ただ、これだけだとまだイメージがつかみにくいかもしれません。
今回は、その「特徴」とは何かを、もう少し具体的に見ていきましょう。

特徴がない問題は、そもそも解けない

まず、次のような問題を考えてみてください。

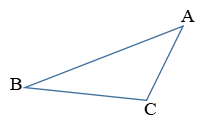
……といっても、何の情報もないただの三角形では解きようがありません。もし知りたければ、分度器で測るしかありません。
つまり、入試や模試でこんな「特徴ゼロ」の問題はまず出ません。
裏を返せば、数学の問題には必ず何らかの“特別な性質”＝特徴があるということです。

直角三角形の「特徴」を洗い出してみよう

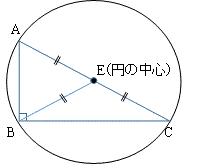
例として、∠Bが直角の三角形 △ABC を考えましょう。
「角の一つが90°」だけで終わらせず、どんな特徴があるか思いつく限り挙げてみます。

まず直角三角形なので、三平方の定理(\( AB^2+BC^2=CA^2 \))が成り立ちますね。

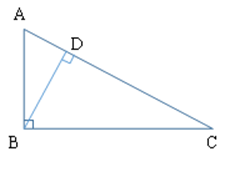
また、直角Bから辺ACに垂線を下した交点をDとすると、△ABD、△BCDはいずれも△ABCと相似の直角三角形になります。

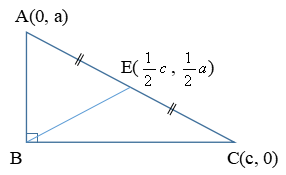
さらに、ACの中点をEとすると、AE=CE=BEとなります。これは、点Bを原点にABをY軸、BCをX軸に重ねて点Aを(0, a)、点Cを（c, 0）とすると、中点Eは(\(\frac {1}{2} \) c, \(\frac {1}{2} \) a)となるので、各々の距離を計算すると分かります。

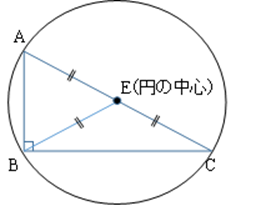
あるいは、ABCの各点を通る円（外接円）を描くと、角Bが直角であるためACは円の直径、Eは円の中心になることからもAE=CE=BE（＝円の半径）を導けます。

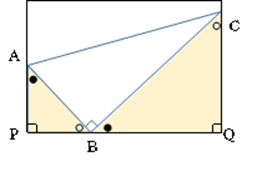
このほか、△ABCが以下のように∠Pと∠Qがいずれも直角の長方形などの中におさまっている場合、△APBと△CBQは相似になります（●をつけた角と〇をつけた角の和が90°になります）。これは直角三角形自体の特徴ではないのですが、他の図形と組み合わせた場合の特徴として、入試問題でもよく見かけます。

特徴はすべて使う！

こうして洗い出した特徴こそが「目のつけどころ」です。
問題に与えられている特徴は、基本的にすべて使うと考えましょう。
2つあれば2つとも、3つあれば3つとも――出題者が使わないヒントを入れることはほぼありません。

入試レベルの問題にチャレンジ！

このブログでは数学の“目のつけどころ”を鍛えるヒントを記事にしているほか、
noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる！中学数学「目のつけどころ」ドリル集
を公開しています（有料）。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます！
ぜひ見に来てください！