数学の問題を解くときの「目のつけどころ」って何？（その1）

「目のつけどころ」って何をすること？

数学の問題を解くとき、最初に必要なのは「目のつけどころ」を見つけることです。
言いかえれば――その“解き方”へとつながる手がかりを見つけることです。

ここがあいまいだと、「こういうときはこう解く」というパターン暗記に頼った勉強になりがちです。もちろんそれも一つの方法ですが、入試で出されるような“ひとひねり”した問題には対応しにくくなります。

私自身が「これが目のつけどころなんだ！」と本当に腑に落ちたのは、息子の受験が終盤にさしかかった1月のことでした。今回は、そのとき息子に話した内容をご紹介します。

ゴールの見えない山道を歩くように

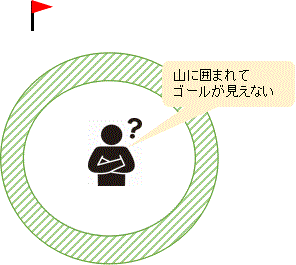
難しい問題では、最初から「これだ！」という解き方が見えることは少ないものです。
感覚的には、山に囲まれてゴールが見えない状態で歩きはじめるようなものです。

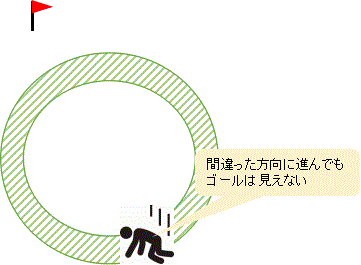
何も考えずに進むと、間違った方向に行ってしまい、いつまでたってもゴールに近づけません。

「特徴」を見つけて考えを進める

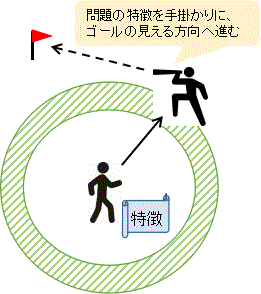
でも、どんな問題にも、必ず「ヒント」となる“特徴”があります。

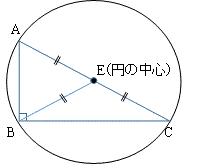
• 数式なら、うまく因数分解できそう
• 図形なら、直角三角形や相似の形が隠れていそう

こうした特徴に気づき、「ここから何が言える？」「さらに何がわかる？」と一歩ずつ考えを進めていく――これが目のつけどころです。

一気に答えまでたどりつけなくても、正しい方向に少しずつ進んでいれば、やがてゴールへの道すじが見えてきます。

模範解答は“最短ルート”

では、その特徴から次のヒントをどう見つけていけばいいのか？
これについては、別の記事で詳しくお話しします。

ちなみに、問題集や模試の模範解答は「こうすれば一直線にゴールできます」という最短ルートを示したものです。
もちろん読むことは大事ですが、「どうしてその解き方にたどり着けたのか？」という理由を自分なりに理解することが、本当の力になります。