すうがくパパ
こちらのコラムでは、三平方の定理を使いこなして空間図形を攻略する方法を解説しました。
しかし、三平方の定理を当てはめるためには、空間図形の問題を解くための平面を切り出す必要があります。
この“平面”をどのように切り出せばよいのか、今回はそのコツをお伝えしたいと思います。
Contents
立方体を切断した断面の面積を求めよう
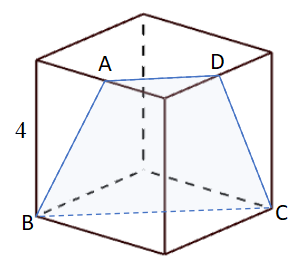
ここでは以下の図のように、一辺の長さが4の立方体を切断した四角形(台形)ABCDの面積を考えてみます。
ここで点A、Dは立方体の辺の中点とします。
立方体を切断面の面積を考えてみましょう
立方体の面はすべて一辺が4の正方形ですから、
\(AD=2\sqrt{2}、BC=4\sqrt{2}\)ですね。
問題はこの台形の高さをどう求めたらよいでしょうか?
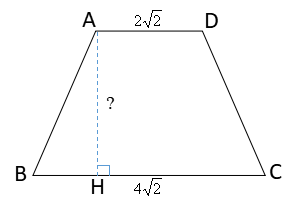
必要な平面を切り出す ─ 長さを知りたい“線分”を含む面に注目
ここで、辺ABを含む立方体の面を見ると、以下のように\(AB=2\sqrt{5}\)と分かります。
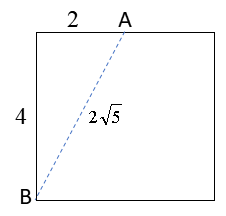
また、ADからBCに引いた垂線の足をHとすると、
四角形ABCDは等脚台形なので、BHの長さは「BCとADの長さの差分」の半分となり、
になります。
したがって、△ABHに注目すると\(AH=3\sqrt{2}\)と分かります。
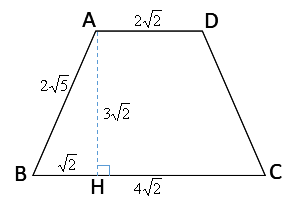
AHを計算!
以上から、台形ABCDの面積は
\(\displaystyle(2\sqrt{2}+4\sqrt{2})\times3\sqrt{2}\times\frac{1}{2}=18\)
と解けます。
立方体の頂点から断面に下ろした垂線の長さを求める
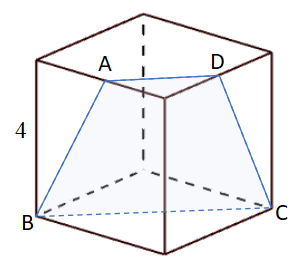
次に、下図のように立方体の頂点Fから平面ABCDに下した垂線の長さを考えてみます。
四角すいF-ABCDの体積を計算した上で、台形ABCDの面積を使って高さを求めることもできますが、ここではもっとシンプルに計算できる方法を紹介しましょう。
どちらの方法にも共通しますが、点Fと平面ABCDとの位置関係が分かるようAB、FG、DCを上に伸ばしてみるのがポイントです。
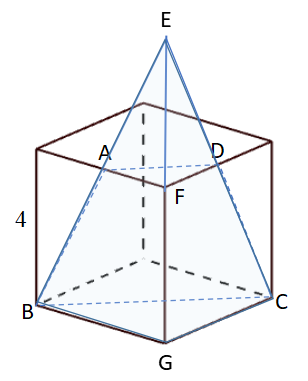
位置関係が見えてきます
AF:BG=FD:GC=1:2なので、AB、FG、DCを上に伸ばすと点Eで交わり、EA=AB=ED=DC、EF=FGの三角すいができあがります。
この三角すいをEBCを底面に置くと左右対称になることが分かります(EB=EC、BG=GC)。
そこでBCの中点をH、頂点Fから平面EBC(平面ABCD)に下ろした垂線の足をIとすると、
点Iは二等辺三角形EBCの中線EH上にあります。
点Hの位置関係を知るために頂点B・頂点Cを含む立方体の平面を切り出すと、このようになります。
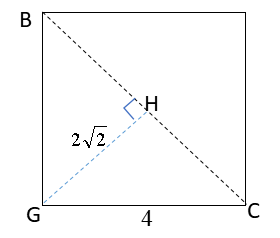
また、点Iの位置関係を知るために平面EBCを切り出すと、このようになりますね。
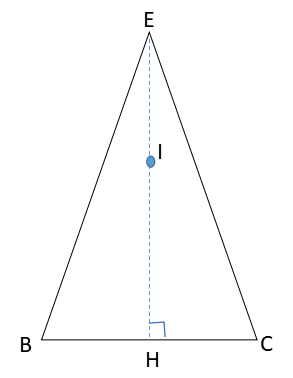
しかし、肝心の頂点Fと点Iとの位置関係は分からないままです。
そこで、点F・点Iを含む平面として、△EGHを平面として切り出してみましょう。
ここで直線FIは平面ABCDに対する垂線なので、FIとEHは直交しています。
また、平面EGHは立方体を垂直に切った形になっているので、∠EGHも直角ですね。
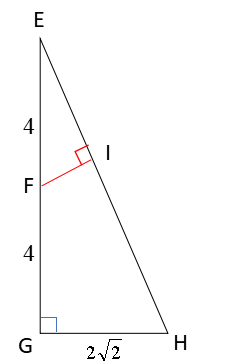
△EGHの切り出しが急所!
相似を使って垂線の長さを求めよう
ここで\(GH=2\sqrt{2}、EF=FG=4\)
で、∠FGHと∠EIFが直角なので、△EFI∽△EGHを利用してFIの長さを求めましょう。
まず、△EGHは直角三角形なので、
\(EG^2+GH^2=EH^2より\)
\(EH=6\sqrt{2}\)です。
また、\(\displaystyle \frac{EF}{FI}=\frac{EH}{GH}\)より\(\displaystyle \frac{4}{FI}=\frac{6\sqrt{2}}{2\sqrt{2}}\)なので、
\(\displaystyle FI=\frac{4}{3}\)となります。
ちなみに、点Gから平面ABCD(△EBC)に下した垂線の足をJとすると、
△EFI∽△EGJ、EF:EG=1:2より、\(\displaystyle GJ=\frac{8}{3}\)と分かります。
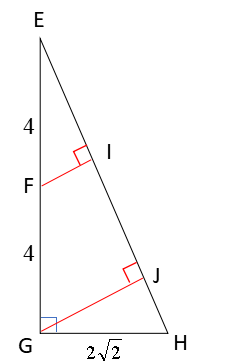
計算できます!
いかがでしたか?
注目している線分を含む平面を「切り出す」ことで、立体のままでは分からない長さを計算することができますね!
次のステップへ!応用問題でレベルアップ!
ここまでで、
「どこに注目すればよいか」
「立体の中から、どんな平面を切り出せばよいか」
という考え方が見えてきたはずです。
ぜひ、次の問題にチャレンジして、空間図形の様々な応用問題に触れてみてください。
入試レベルの問題にチャレンジ!
また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる!中学数学「目のつけどころ」ドリル集
を公開しています(有料)。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます!
ぜひ見に来てください!