すうがくパパ
「赤玉3個と白玉2個を並べます。並べ方は何通りありますか?」
中学の「場合の数」でよく出てくるタイプの問題ですが、
実は考え方の“入り口”がいくつもあることに気づいている人は多くありません。
今回はこの問題を、
- 白玉をどの位置に置くかで考える
- 赤玉をどの位置に置くかで考える
- 左から1番目→2番目→…と、順番に考える
という3つの方法で検証してみます。
同じ答えになることを確認しながら、「どこに目をつければよいか」を一緒に整理していきましょう。
Contents
はじめに:赤玉3個・白玉2個を並べると何通り?
今回考えるのは、この問題です。
赤玉3個・白玉2個を、左から一列に並べるとき、並べ方は何通りあるでしょう?
赤玉どうしは同じ、白玉どうしも同じと考えます(=区別しない)。
つまり、
「赤白白赤赤」
のように、赤と白の並び方だけが問題になります。
この問題は、考え方の入り口が3つあるのがポイントです。
どれを使っても同じ“答え”にたどり着くので、
「どうやって数えれば重なりなく・漏れなくなるのか」を体感できます。
今回は、次の3つの視点で数えてみます。
- 白玉の位置に注目する
- 赤玉の位置に注目する
- 左から順に決めていく
方法① 白玉を置く場所に注目する
まずは「白玉の位置」に目をつけます。全部で5つ場所があります。

この中から、
白玉を置く場所を2つ選べば、あとは全部赤玉になります。
たとえば、
- 白が1・2番目
- 白が1・3番目
- 白が2・5番目
- 白が4・5番目
などです。
つまり、
「5つの中から2つ選ぶ」
という組み合わせを考えればOK!
この選び方は全部で
\(5\times4\div2=10\)ということで、10通り あります。
白玉の場所が決まれば残りは全部赤玉なので、
並べ方の数も 10通り です。
方法② 赤玉を置く場所に注目する
次は「赤玉の位置」に注目します。
赤玉は3個なので、
5つの場所から3つ選んで赤玉を置くことを考える方法もあります。
この選び方も
\(\displaystyle\frac{5 \times 4 \times 3}{3 \times 2} = 10\)ということで、10通り と計算できます。
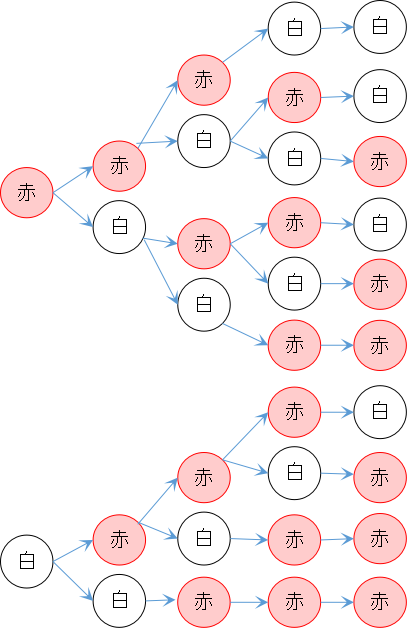
方法③ 赤玉・白玉の置き方をツリー図で整理する
赤玉3個・白玉2個を左から順に並べるとき、
「1番目には赤?白?」というように、ツリー図で整理する方法もあります。
今回の場合、最初の二つは赤玉・白玉のどちらも置くことができますが、
そこから先は
- 赤玉を3個使い切ったら、残りは白玉だけを置くことができる
- 白玉を2個使い切ったら残りは赤玉だけを置くことができる
という点に注意しましょう。
実際に書いてみると、やはり10通りになっていますね。
次のステップへ!応用問題で発想をレベルアップ!
赤玉3個・白玉2個の並べ方を、
- 白玉の位置で考える
- 赤玉の位置で考える
- 左から順に決めていく(在庫を意識する)
という3つの視点で整理できたら、
場合の数の“考え方の土台”がしっかり身についてきています。
ここから先は応用問題にチャレンジ!
色の玉の並べ方だけでなく、じゃんけん、カード、サイコロなど、
いろいろな「場合の数・確率」の問題で発想力をアップさせましょう。
入試レベルの問題にチャレンジ!
また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる!中学数学「目のつけどころ」ドリル集
を公開しています(有料)。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます!
ぜひ見に来てください!