関数の問題は、
「計算はできるのに、なぜか点が取れない」
と感じる人が多い分野です。
入試で問われる関数は、
単なる式の処理ではありません。
グラフをどう読み取り、何を手がかりに考えるか──
その見方ひとつで、解きやすさが大きく変わります。
このページでは、
入試レベルの問題を通して、
関数を解くための「目のつけどころ」を鍛えていきましょう。
関数でつまずく理由とは?
関数が苦手になる原因の多くは、
式とグラフを別々に考えてしまうことにあります。
入試問題では、
- 変化の様子
- 交点の意味
- 増減や傾きの関係
といった、
グラフから読み取れる情報が重要になります。
式だけを追いかけていると、
何を求めればよいのか分からなくなり、
途中で手が止まってしまうことも少なくありません。
関数攻略のカギは「グラフを見ること」
関数の問題では、
まず グラフを丁寧に見ること が大切です。
- どこで交わっているか
- どの部分で増えているか、減っているか
- 変化の仕方が切り替わる点はどこか
こうしたポイントに注目すると、
問題文で聞かれている内容が整理されていきます。
「このグラフは、何を伝えているのだろう?」
と考える習慣がつくと、
関数は一気に解きやすくなります。
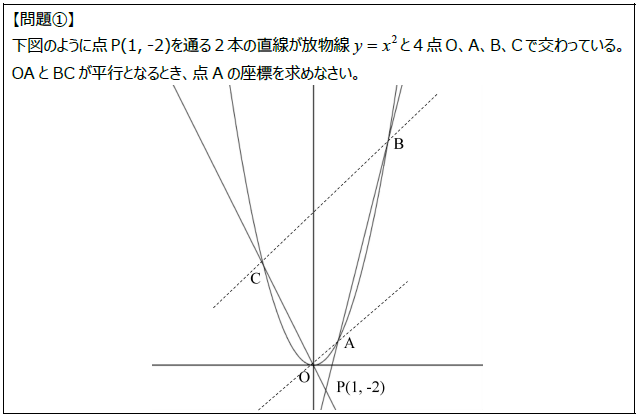
問題にチャレンジしてみよう
それでは、実際に問題に取り組んでみましょう。
解き始める前に、次のことを意識してみてください。
- 先に計算せず、まずグラフを眺める
- 変数が変わると、何がどう変わるのかを考える
- 式とグラフの対応関係を確認する
「どこを見るか」 がはっきりすれば、
解くべき内容が自然と見えてくるはずです。
関数の本質は「関係を見抜き、動きを想像する力」。
式をただ変形するだけでは、関数の応用問題は突破できません。
グラフ・図形・文章に隠れた“つながり”をどう見抜くか――
その発想こそが、関数の「着想力」です。
詳しい解説と解答は、こちらからダウンロードしてください。
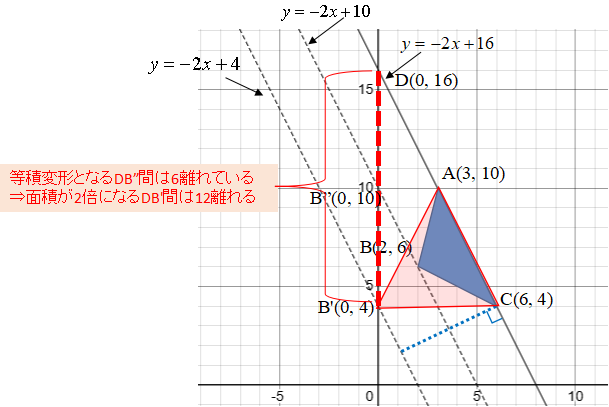
この問題のカギは、「平行」から「相似」へつなげる発想でした。
放物線の応用では、数式だけで押し切ろうとせず、
まず図形的な関係(平行・比・対称)を手がかりに整理することが重要です。
次のステップへ|関数を得点源にするために
さらに関数の着想力を磨きたい人のために、
noteに関数問題編のドリル(有料)を用意しています。
入試本番で差がつく放物線・一次関数の融合問題を厳選し、
「どんな関係に注目すればよいか」「どう整理すればスムーズに式を立てられるか」を丁寧に解説。
読むだけでも“関係を読み解く力”や“動きを想像する力”が鍛えられます!
noteでは「数式」「関数」「平面図形」「空間図形」「場合の数・確率」の各分野を公開中。
苦手分野を集中的に克服したい人も、体系的に学び直したい人も、
解き方が見つかる!中学数学「目のつけどころ」ドリル集 をぜひチェックしてみてください!