九九の総和はいくつ？身近な疑問を数学的に考える

小学校で習う九九（1×1、1×2、・・・・、9×9）をすべて足し合わせると、いくつになるのでしょうか？フツーに考えると、結構難しいですよね。

まずは1から9までの足し算を整理しよう

これを考える前に、基礎問題として
1から9までの整数の総和（1+2+3+4+5+6+7+8+9）がいくつになるか、考えてみることにしましょう。

ここで、1+2+・・+9と、この順序をひっくり返した9+8+・・+1を足し合わせると、

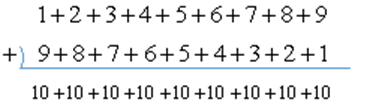
となり、10を9つ足し合わせて90になると分かります。ですから、1+2+3+4+5+6+7+8+9は、その半分の45になります。

九九の各段を足すとどうなる？一の段から九の段まで

さて、本題の九九です。まず、一の段の総和を考えてみると
(1×1)+(1×2)+・・・+(1×9)=1×(1+2+・・・+9)　　（①）
になりますね。

同じく二の段の総和は、
(2×1)+(2×2)+・・・+(2×9)=2×(1+2+・・・+9)　　（②）
になります。

同じく、九の段の総和は、
(9×1)+(9×2)+・・・+(9×9)=9×(1+2+・・・+9)　　（③）
となりますね。

九九の総和を式で表すとこうなる

ここで①~③の右辺に注目すると、九九の総和は
1×(1+2+・・・+9) + 2×(1+2+・・・+9) + ・・・+9×(1+2+・・・+9)
=(1+2+・・・+9)×(1+2+・・・+9)　　（④）
になります。

答えは2025！きれいな関係が見えてくる

さて、冒頭で説明したように、1+2+・・+9=45ですから、④より九九の総和は
45×45 = 2025となります。

九九から学べる「発想力」のヒント

九九の総和を求める問題は、一見すると単純な計算の積み重ねに見えます。
しかし、少し視点を変えるだけで「全体の構造」に気づくことができます。

たとえば、段ごとに同じ「1＋2＋…＋9」が出てくることに気づけば、
複雑な計算も一つの式にまとめられる――
まさに“パターンを見抜く力”＝発想力 のトレーニングです。

数学の面白さは、正解を出すことよりも、
「どう考えたらうまく整理できるか」を発見するところにあります。
身近な九九にも、そんな“考えるヒント”が隠れています。

次のステップへ！応用問題で発想をレベルアップ！

九九の仕組みがわかったあなたなら、
もう「数式の世界」に踏み出す準備はできています。

入試レベルの数式問題にチャレンジ!では、
式を使って考える練習問題にチャレンジできます。
「どうしてこうなるんだろう？」と感じたその気持ちを、
数式でスッキリ整理してみましょう！

入試レベルの問題にチャレンジ！

また、noteでは、ハイレベルで入試本番にも頻出しそうな応用問題を厳選した
解き方が見つかる！中学数学「目のつけどころ」ドリル集
を公開しています（有料）。
「目のつけどころ」を丁寧に解説しているので、読むだけでも発想力・着想力が鍛えられます！
ぜひ見に来てください！